Random Events
From May 05, 2020
Considering that an event A can occur with a probability p=p(A).
From probability’s theory we know that uniformly-distributed probability at [0:1].
One random value fits into the interval with length p inside the range [0:1] so in this case P{α < p} = p = P{A}
α is generated by the base generator, according to the following:
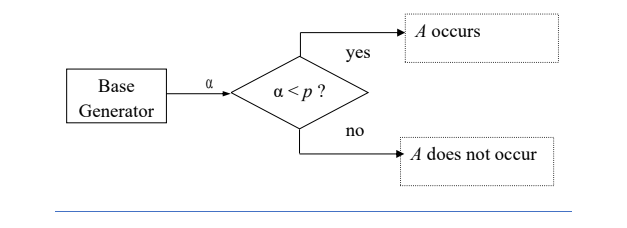
Base generator
Random rand = new Random();
int n = rand.Next();
string answer = "No";
if (n % 2 == 1)
{
answer = "Yes";
}
Group of events
Given A1, A2, . . . , Am as a collective group of events, we have that P{Ai} = pi where i=1 ∑m pi = 1 dividing the interval [0;1] into intervals of length pi
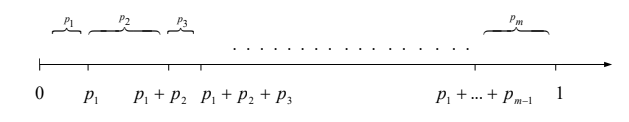
We can use the property that uniformly distributed probability at [0;1] on the random variable matches with the interval of length p inside of [0;1] and is equal to p.
So now we have the algorithm as follows:
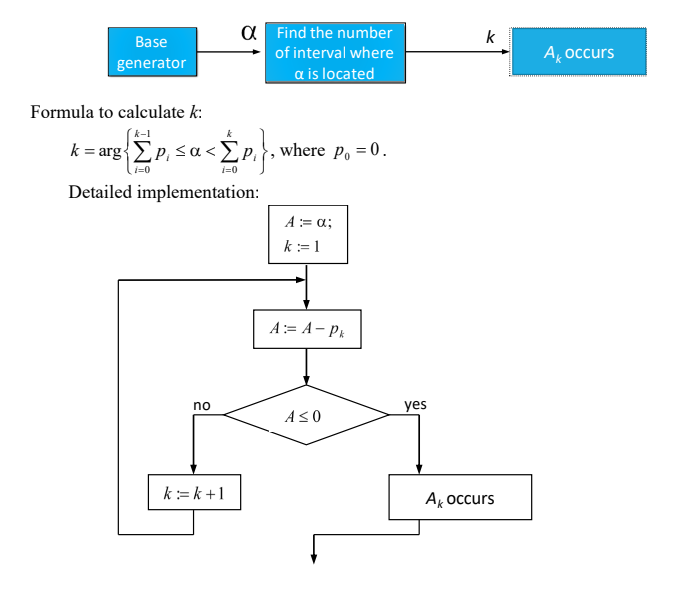
Result
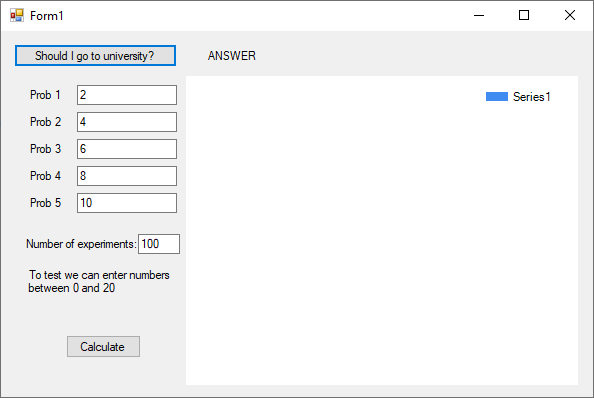
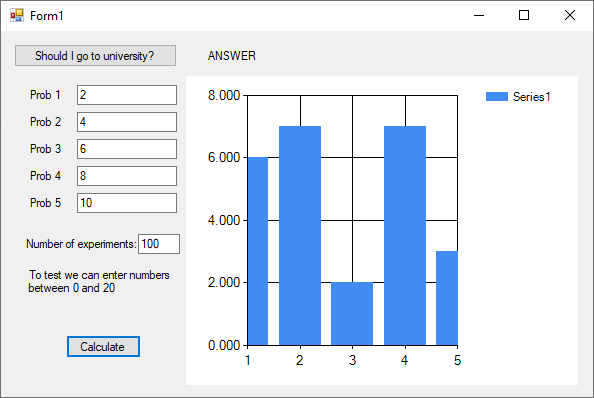
Implementation
int i = 0;
int n1 = int.Parse(textBox1.Text); // Prob 1
int n2 = int.Parse(textBox2.Text); // Prob 2
int n3 = int.Parse(textBox3.Text); // Prob 3
int n4 = int.Parse(textBox4.Text); // Prob 4
int n5 = int.Parse(textBox5.Text); // Prob 5
int n = int.Parse(textBox6.Text); // number of experiments
int[] experiments = new int[5];
double[] frequency = new double[5];
experiments[0] = 0;
experiments[1] = 0;
experiments[2] = 0;
experiments[3] = 0;
experiments[4] = 0;
while(i < n)
{
int r = rand.Next(20);
if (n1 == r) experiments[0]++;
else if (n2 == r) experiments[1]++;
else if (n3 == r) experiments[2]++;
else if (n4 == r) experiments[3]++;
else if (n5 == r) experiments[4]++;
i++;
}
i = 0;
foreach (var item in experiments)
{
frequency[i] = item / 20;
}