Wiener Process
From June 22, 2020
In a Wiener process w(t):
- If the time intervals
[s, t]and[s', t']do not intersect, then the incrementsw(t) - w(s)andw(t') - w(s')are independent random variables. - As the increments
w(t) - w(s)are normal random variables withE{w(t) - w(s)} = 0andVar{w(t) - w(s)} = t - s
This way we have that w(ti+1) - w(ti) ~ N(0, ti+1 - ti) for the simulation.
Simulation
Given a normal random variable w(ti+1) = w(ti) + √(ti+1 - ti) due time instants ti is posible to pick them as we see fit, as the moment in which two instants are -sufficiently short- to match to other process simulated on the system.
Brownian Movement
Is given by the following equation:
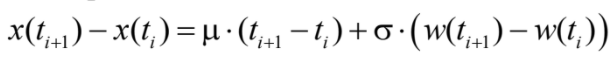
For the simulation we will use
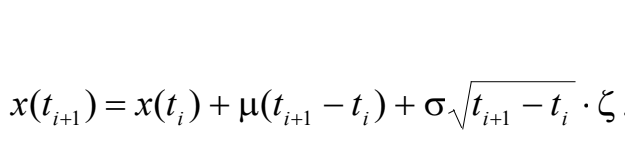
Geometric Brownian Movement
Is given by the following stochastic differential equation
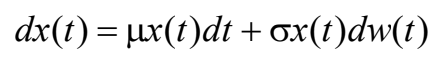
Its solution can be written in the following way
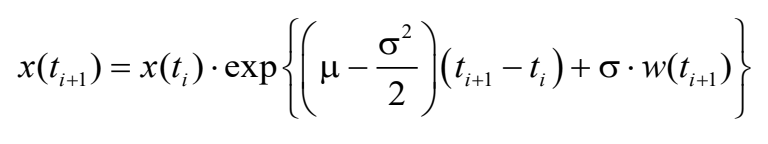
Result
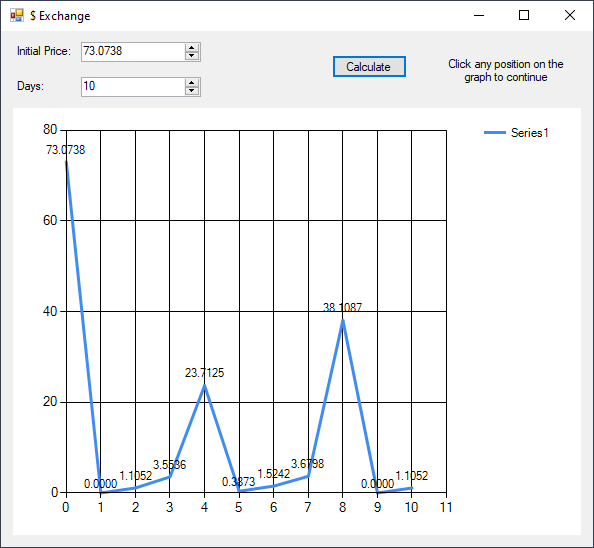
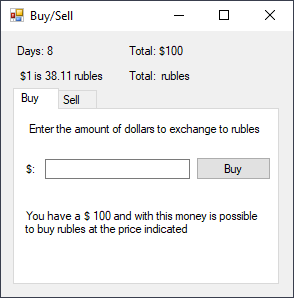
Implementation
Random random = new Random();
const int miu = 1;
const double k = 0.1; //0.02
int days = (int) inputDays.Value;
double price = (double) inputPrice.Value;
chart1.Series[0].Points.AddXY(0, price);
for (int i = 1; i <= days; i++)
{
//price = price * (1 + k * (random.NextDouble() - 0.5));
// e^((miu - (price*price/2)) * k + price * random)
double w = miu + Math.Sqrt(k) * (random.NextDouble() - 0.5);
price = Math.Exp((miu - (price*price/2)) * k + (price * w));
chart1.Series[0].Points.AddXY(i, price);
}